Ahhh 2020… the gift that just keeps on giving…
London went back into lockdown at the start of November, which to be fair, a lot of people were predicting. So it didn’t come as much of shock to most people but it still sucked. But what really felt like a Tyson uppercut was when one of our flatmates came home saying she had tested positive for Covid … 😱
She’s a Covid nurse who has to get tested multiple times a week but the funny thing is that she’s already had Covid before (she’s had the antibody test) and was certain she didn’t actually have it this time. Apparently false positives are not uncommon and it’s what most likely happened. Regardless, as a result, the whole household had to stay inside for two weeks straight without leaving the flat 🤪🤪🤪
The obvious question I had straight away was couldn’t she get tested again to make sure she actually has it? But the protocol states that even if she gets tested 100 more times and they all show up as negative, that one positive overrules everything and we all need to self isolate for two weeks inside without leaving… 🙃…goooooooood
I was already mentally preparing for the two weeks quarantine we are still going to have to do next month when we return home but this really took us by surprise and I was not ready for it at all! I’ve got a skipping rope and was still able to do bodyweight exercises but the lack of sunshine and fresh air really got me down towards the end there.
Because we were locked inside for two weeks, I started to look at gaming systems on Gumtree and thought maybe we can pick one up pretty cheap to help get us through the lockdown. After a bit of research, I decided to get a subscription to a cloud gaming service by Google called Stadia. Hopefully, there are some gamers who read this blog because let me tell you, as a former relatively hardcore gamer, I couldn’t believe that this tech even exists and works so well.
I’ve been eyeing off the new PS5 for a while and there was a pretty good chance I was going to buy one next year but after trying this cloud gaming stuff out… I’m almost certain these latest consoles will be the last ever made. Maybe this is a bold statement but I can’t see how all gaming doesn’t move to the cloud over the next few years.
When you sign up to Stadia, you get given a controller and chrome cast. That’s it. No console!
The controller connects directly to your WiFi and the chrome cast enables your TV to stream the game video. But because the computing and graphic rendering are done in the cloud, the screen that you actually game on can change. It’s so cool and works so well! I can play Red Dead Redemption 2 in the living room (small flex for London that we have a living room ps 😜) but move upstairs to my computer’s 27 inch if the girls want to watch a movie. It even works on your phone/iPad. Because the controller is connected to the net and not a console, you just have to pair the controller with your screen and boom, off you go!
I was also really attracted to fact that you don’t need a subscription to play Stadia games online (unlike Xbox and Playstation) and no big outlay to buy a physical console, the only cost is buying the controller and games.
I promise you I’m not an undercover Google employee because it probably sounds like I’m trying to sell the system. I’m just a tech nerd at heart who works with a lot of cloud technologies and was really impressed at an engineering level that something like this can even exist. Absolute madness!
Stadia just needs to get COD on their system as the lack of zombies was my only gripe 🧟♂️🔫
Net Worth Update
Ho ho ho, did Christmas come early this year 🎅?
Over $50K in gainz from shares and Super which hid an otherwise extremely expensive month since we booked our last holiday and flights back home for next year. I know there was some really positive news on the Covid vaccine front but it’s pretty insane how much the share market went up in November. It’s funny to look at some of the comments that were flying around in March/April. Covid is just another nail in the coffin for trying to time the market.
How many of you guys out there are still on the sidelines waiting for the next drop? What happens if the markets never drop below what they are at right now huh? We all know that eventually, they’re going to reach new heights, but new bottoms are never guaranteed.
All this printing of money does make me wonder about the long term outlook for fiat currencies around the world. I sleep so much better at night knowing the majority of our wealth is stored in businesses and real estate. Don’t get me wrong, having cash on hand is handy. But I can’t help but feel the purchasing power of my emergency account is copping a flogging every time the government drops some sort of stimulus.
Properties
Since it is related to property (just not in the investment sense) I’ll add it in this part…
I’ve been looking at home loans recently and have been blown away at how low an interest rate you can get on a fixed mortgage. We have been looking at houses since the start of the year because we want kids one day and I’ve been crunching the numbers on renting vs buying for our area and the results are leaning towards buying which shocked me a bit. Much of this has been driven by low-interest rates though. I’d love to know who you guys are with and what rate your paying (also if it’s fixed or variable) in the comment section, please 🙂
Property 1 was sold in August 2018
*DISCLAIMER*
The current value of our properties is a rough guesstimation based on similar surrounding properties. I only really update these when we get an official bank valuation
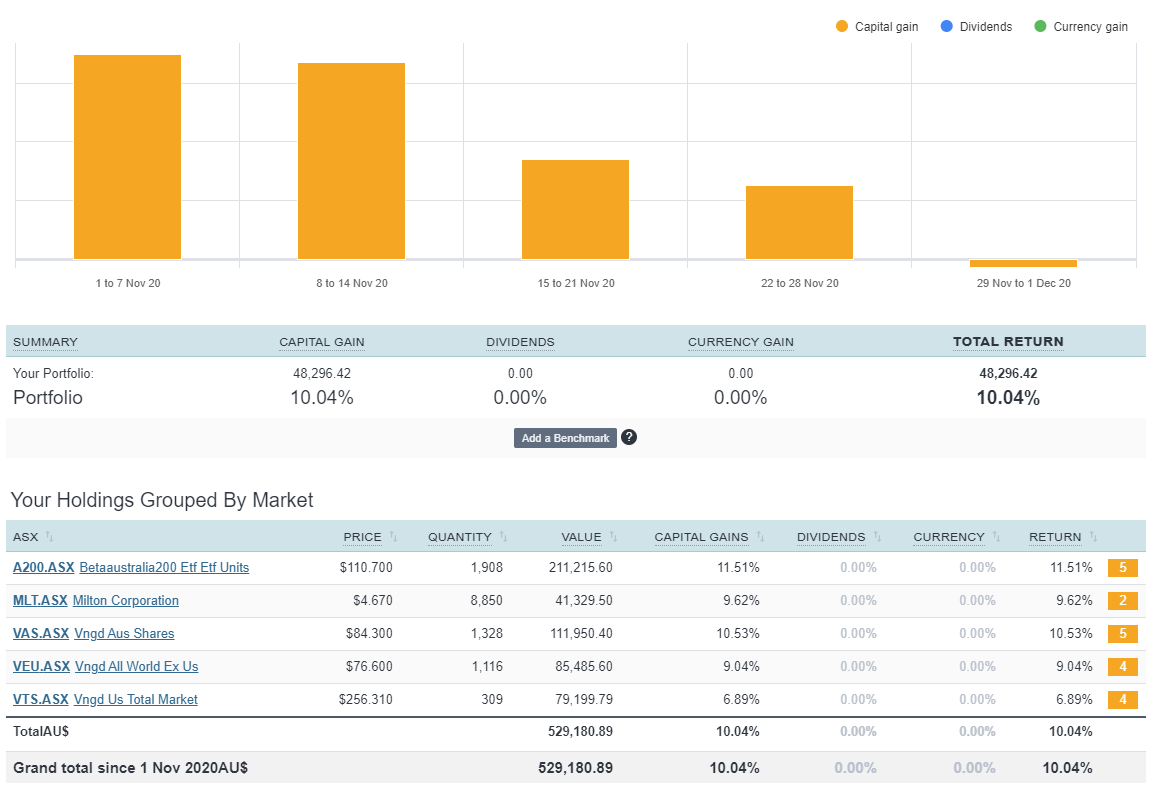
ETFs/LICs
The above graph is created by Sharesight
Wowzers!
The ASX goes bang in November.
I was thinking about this the other day. An investor’s reaction to sharemarket movements can be a reflection of their personality in many ways. You see, it doesn’t matter what the sharemarket does, I always find a reason to be happy about the result.
If it drops, that’s awesome! I can now pick up great companies at a reduced price. If it rockets upwards, that’s also great, look at how much wealthier we just became. Even if it goes sideways I usually can pick out some positive in the markets low volatility and how good it is 😅
I’m an optimist at heart and investing/life is a lot easier if you have a positive mindset. I truly believe that!






That’s great progress!
Completely agree that a positive mindset is critical in dealing with accumulation in volatile times. Avoiding regret, and focusing on the fact that more assets are now working harder towards your FI objective is really important.
When markets are travelling along sideways (which hasn’t been an issue recently!) I often think ‘I can’t believe I can still accumulate these same income producing assets at the same price as last month’.
That’s a great find on the gaming front – as someone who accumulated old consoles back to N64s, it does sound like the future! 🙂
Mindset is everything!
Ahhhh the Nintendo 64 ♥
My favourite console of all time which will never be beaten (mainly due to nostalgia reasons).
– Mario 64
– GoldenEye
– Super Smash Bros
– Mario Kart
– Banjo Kazooie
– Zelda
The mindblowing concept of being able to game with 3 of your mates on the same system at once 🤯. The N64 will always have a special place in my heart
With the property graphs, what does the blue and red sections mean?
I’m reading this off my phone and it doesn’t seem to display all details.
Blue is how much the property is worth and the red is the debt associated to it.
Love the progress and the dig at market timers. I’m a firm believer in empirical evidence and almost every piece of data on market timing undeniably points to it being impossible to do consistently. As the late Vanguard founder, John Bogle, once said, “The idea that a bell rings to signal when investors should get into or out of the market is simply not credible. After nearly 50 years in this business, I do not know of anybody who has done it successfully and consistently.” Throw it in an index and check your annual statement and you’re set.
I still have my N64 from the 90’s with Golden Eye, Super Mario 64 and Mario Kart 64. Nostalgia to the max!
My offer to help on the podcast editing front still stands if you’re interested!
Cheers Dylan.
I sold my old N64 nearly 10 years ago for quite a bit of money actually. I had a few rare games that went for nearly $200 a pop which I was blown away by. Out of curiosity, I just checked on Amazon for what it’s going for and the asking price is over $1,000 AUD 😲
You might be sitting on a goldmine mate.
And yes… and I want to take you up on the offer but I’m not doing any AFB podcast stuff until next year mate. I’ll get back to you via email 🙂
It’s certainly not in anything new mint condition – heavy use from ages 6-15 tend to do that to a console. But at least it still runs. I’m not sure I could ever get rid of it.
Not a problem, mate. Look forward to hearing from you! Have an awesome Xmas period and hopefully you can finally spend a little time outside haha!
Love your updates!
I fixed my IP with ANZ for 1 year at 2.39% back in June.
And you probably have a 100% offset account on that too! Winning 🙂
You cannot have a 100% offset with a fixed interest rate, one of the many drawbacks of a fixed loan.
The bank draws you in with a lower rate, however most of the time (especially if you have any savings to have in an offset) you are better off with the variable rate.
Actually yeh you can, with ANZ 1yr fixed rate. It’s a cool perk of theirs 😉
We’ll I’ll be, that’s a ripper deal then.
Maybe I will get amongst it, O wait I can’t cause a portion of my loan is fixed 🙁 (I have learnt the hard way, and yes I have done the math’s and the break fees are more then what I will save..)
Similarly at Bank Australia (which I’ve switched to for ethical reasons)–100% offset, AND 2.19% fixed for 3 years.
Are you able to share a link for more details on this fixed loan? Thanks.
https://www.bankaust.com.au/personal/borrow/home-loans/premium-home-loan-package
Their current 3yr “fixed” rates are 1.99% Owner Occupied or 2.39% (I think) for investment.
Thanks! That’s a great rate 👌
Well done!
Great rates at the moment. You can get 1.99% fixed and still make extra payments depending on the lender. I have also fixed my investment properties at 2.39% with Macquarie and 2.49% with Westpac 2.19% with CBA.
1.99% is crazy low! What a time to be alive!
Can get 1.8s for 4yrs with Bank of Melb/St George. Full disclosure: I own a mortgage broking business. Not a sell just a heads up
Crap forgot to mention…. with a $4000 cashback!
Hey Lee a question here if you would know.. is that rate possible for investments and in a trust structure? Great rate!
Sorry Humna that was an Owner Occupied rate. Probs more like 2.2s for investment but would need to check on whether trust lending OK with the specific lender when digging further
Personally, having recently come off fixed and I won’t fix again particularly for a PPOR, it limits you ability to make extra repayments. Investments maybe, however if you are looking to sell or change anything etc. then you have very little flexibility. Also many of the comparison rates are a lot different to the advertise rate.
I just refinanced with CUA – 1.97% fixed for 3y.
what an incredible year it has been!
the first year on our FIRE journey and we have had a global pandemic that is still underway, a crazy US election that is somewhat still underway, and yet we are going to make significant gains in our portfolio!.
all the evidence we need for time in the market > timing the market.
I don’t think anyone will be forgetting 2020 anytime soon!
Wow, great month for you and bummer about the unexpected lockdown. We all think it would be nice to have to stay at home, until we are forced to lol. At least you’ve got your trip to look forward to.
As someone who is just about to start some regular monthly investing in ETFs & LICs, can I ask how you decide where to direct your money each month across your 5 different options? Do you look at the share prices of each and funnel the money to the one with the lowest price at the time or do you have a set 5 way disbursement formula that you use each month? I hope that makes sense. I’m a newbie but keen to learn, am reading as much as I can but don’t want to get analysis paralysis and sit on my hands haha.
Great questions Lisa.
We are currently trying to aim for a portfolio that consists of 70% Australian shares, 15% US and 15% world ex US.
I look at our net worth spreadsheet each month (download at the end of these articles) and it breaks down our portfolio into those three splits I mentioned above. The next buy order will top up whichever split (out of the three) is the lowest from it’s target weighting.
We buy A200/VAS for the aussie part, VTS for US and VEU for world ex US.
Hope that makes sense 🙂
Cheers
Stadia is not available in Australia – at least that’s the message I got when I looked today from Sydney. Typical!
OMG I didn’t even check that… NOOOOOOOOOO… now I can’t play during quarantine 😭😭😭😭
You could set up a VPN via Surfshark which apparently let’s you set your “location ” to any place in the world to access content. No affiliation just see it plugged by KARA & NATE, the American travel bloggers- they are often sponsored by surfshark and have discount codes for it.
I have read about this but apparently, the ping is just not good enough. I’m happy to wait for Stadia to hit Australia this year hopefully.
Hey man, awesome to hear you’re and the household is safe. Bit of a gamer need here and heard about stadia a while ago but assumed with the issue of high latencies in standard client side games, I imagined this tech would be years off before taking over.
Great to hear first hand experience. Love the updates bud. And travel back safely.
Cheers mate.
Apparently Stadia had a really bad launch when it first came out last year. From what I’ve read, the latency issues have been greatly improved and I can personally say that we had three people all streaming Stadia in one flat and it worked perfectly.
If you plug in the ethernet cable to your chrome cast, you should get 4K resolution with 60 FPS. Playing RD2 on the TV is stunning! I can still play on WiFi but the resolution is the first thing Stadia will drop if there are network issues.
Maybe Australia’s ping is too high for it to work right now but our flats internet in London is good but nothing amazing and it still works great.
Total bummer about the flat mate getting a positive test result. At least with your next holiday you can make up for lost time with a few extra beers.
Are you looking to buy your new house with the equity of your investment properties ?
I am with Homestar Finance 2.14% P&I, over 80 LVR variable and Reduceloans 2.14% P&I over 80 variable. Took a but of haggling with reduceloans.
Cheers FDU.
Yes, that’s the plan for now (it keeps changing).
I want to sell a property or two next year and dump all that cash into a home loan and then rip it out straight away to invest in shares (AKA debt recycling). Big post as I do it next year if it happens 🙂
Hi does your net worth include you and your partner? If question is too personal no worries just ignore. Id like to see how im tracking with or without my partner compared with our fire leader to give me a FIRE reference point. Thanks
No worries at all.
These net worth posts were solely mine up until September 2016 when my partner and I joined finances. From that point onwards, it has been a joint effort and I can tell you right now that my NW wouldn’t be half of what it is today without her. So much easier as a team!
Re:Home Loans
We are Brisbane-based and have had our PPR loan since 2016. Interest rates have fallen a lot since then and we find the ultimate flexibility with sticking on variable for our PPR. Yes, we pay a tad more interest (currently 2.89%) but I remember paying 6.5% in 2010 and the oldies all tell us about the 20% days in the 90’s! So the flexibility to be able to make unlimited extra payments, have instant redraw facilities AND an offset account is too good to pass up for us. Also if your situation changes and you want to sell or restructure your loan – the break fees with fixed can be exorbitant. We learned that the hard way when we had initially 80% of our PPR loan fixed and 20% variable – sold an IR unexpectedly and wanted to lump sum pay down – had to pay a $1400 break fee- not too bad but annoying.
We’ve smashed our loan from 580k in April 2016 to 140k today and fixed is just too inflexible for those of us with quick repayment in mind. We currently pay $1400 less per month in interest than we did when we started this loan. Nice tax free pay rise! We do use fixed loans on our IPs- one year at a time at the moment, P&I. I stupidly fixed an IR loan for 3 years in 2017 on interest only 4.29% – ouch. Since switching to 1 year fixed via our broker on 2.69% P&I, we are paying only $300 more a month for the payment, but smashing over 1k per month off the principal. So, it’s a case by case thing!
Arghhh mate gutting on the enforced lockdown for your flat! Having said that, a separate lounge room in London? Are you even doing FIRE if you’re not in a share house with 3 bedrooms (one of which is a converted lounge room) and 6 couples all packed in together? You need to up your frugal game! 😉
Congrats on smashing the $800k mark, it was a pretty good month for us as well! Nice to be hitting all time highs!
I had a mate that slept on a staircase for a few weeks before getting sorted lol.
Most of my mates did the whole London thing straight out of uni though. Like… I’m a pretty frugal guy, but not Uni level frugal anymore 😂
Interesting… it’s almost like this isn’t about a virus?
Hope you guys pull through OK.
Yeah it’s not ideal with your housemate situation, hope it all works out!
A big gamer here, not professional cause my reactions are too slow although I do get play against some pros sometimes on Ranked AOEIIDE ladder. 🙂 Yeah I’m looking forward to Stadia reaching Australia and surprised you only just heard of it. Maybe we can do a FIRE Community gaming session at some point if there’s enough interest! I’m also into COD and other FPS.
I’m currently doing a monthly newsletter for the Aus FIRE community which includes the updated cheapest rates in the market so people can always check how their rates are looking and as everyone situation varies depending on LVR, loan type etc and hopefully mine can be used for all scenarios. Let me know if you think the format is useful for you:
https://www.thefirenanceguy.com/post/the-fire-trial-october-november-2020-newsletter
Disregard the crappy structure and design, I’m currently getting it re-done and turning the google sheet tools into webapps. I just want to create something that people will find useful and that it will help reduce some of the bigger household items.
Hoping you can enjoy the rest of your time away from Australia as best as you can!
Nice one. I’d definitely be down for a COD session!
Hey mate from the table above does it mean you haven’t made any ETF / LIC investments since Dec 2019 as thats the earliest it shows as bought 5K ETF ? Havent you been timing the market then or is there anyother reasons to stop investing since then ?
Oh crap, I forgot to say what we actually bought last month 🤦♂️.
We have been buying pretty much every month for the last 4 years.
We bought around $10K worth of VTS in November mate.
Wow how do you manage to buy 10K worth ETF every month
A build up of cash.
We usually aim to buy around $5K a month.
Hey mate, take a look at FreedomLend, currently offering 1.97% variable LVR ≤ 70% or 2.19% variable LVR ≤ 80% with an Offset, no ongoing fees. I’ve been happy with them for the last 4 years. Best part you get straight through on the phone and deal with the same person each time.
Wow that’s a good rate. I’ll definitely have to look into it. Cheers
Wow lemme just say your track record of your financials is impeccable. I wish mine was like this seems overwhelming. I’m looking into getting into ETFs next year. You are helping so many people you have no idea.
Appreciate that Michelle 🙂
Thanks
Great to see your planning ahead for your families future housing needs. I’ll be interested to see how you go about financing the purchase of your family home.
Cheers Bart.
I’ll be making a post about the PPOR when/if we find something next year
Are you on Warzone FB? Maybe we should setup a FIRE team! =)
Nope. I’m really just a COD and SC2 gamer really. I am enjoying Red Dead 2 atm though
For the silver lining – You will be well prepared for the quarantine period coming in to Oz 🙂 Hope it’s not too bad. I’m sure it will be nice to be home. Loving this stock market rally!
Google did a pretty awful system for buying games though. You have to buy them on their store. This means you can only play it on Stadia. Whereas with GeForce now and other ones, you use your own games on Steam and b.net etc, so you own the games and aren’t as limited. It also seems Stadia is pretty hit or miss for the lag depending on where you live and no support for Australian customers either
I hear ya, but the best thing about Stadia is you can play it anywhere (as long as it’s available in your country). You don’t need to have a subscription either… so in a sense, you really aren’t limited at all. All I’m waiting for is COD to come out with cross platform support. If I can play my mates on PS5/Xbox… that’s all I’ll ever really need!
The lag was a big issue at the start (from what I’ve read), but I can personally vouch that it works really well here in London. I guess we’ll have to wait and see what happens with the Australian infrastructure.
Mate Ive been talking to the boys bout yer blog mate and we all wanna start dabble in some stocks in an round the usual sportsbet / pokies (supplement our portfolios). good to see ya all in on stocks and property don’t worry bout cash mate PE ratios are sky high and bound to get higher before yer gonna need to sell don’t be a pussy. Keep it up champ let me know if yer need a hand editing ya blogs or any welding jobs mate
I do enjoy Dazza’s comments… Slipping a pineapple or two into Cleopatra is the safest investment in 2020.
Appreciate that Daz.
I’m not too bad on the tig myself mate 😉 but I’ll yell out for the big jobs
Hi,
Just wanted to drop a comment regrading the potential Sydney meetup discussed on one of the monthly updates a while back.
I’d think I Aussie Firebug beer/schnitzel at the pub could be good fun.
My AFB inbox is out of control atm so apologies for not getting back to you. Maybe flick me another email to move it up the pile and I’ll take a look 🙂
Just started tuning in AFB this week and enjoying it. Ive been with loans.com for several years which is an online lender. I know its not the lowest rate i could get if i swapped lenders as a new customer but I’m at PPOR 2.5% and IP’s 2.9% variable rates with offsets. Best thing is though i got 25 basis points off PPOR and 60 basis points off from a simple phone call the other week. I did the same thing 3 months ago and got a reduction at that point in time too. Pick up the phone!!!
I got my very first home loan with CBA mid 2019 at 3.79% variable and with all the subsequent drops is now down to 3.08%. I have just fixed ~80% at 1.99% for 4 years and left the rest variable, which is the goal value of my emergency fund and will be entirely offset within a few months. For the next 4 years I will make the minimum payment (which is over $400 a month less than when I started!) leaving me free to dump all my extra cash into ETFs. I can’t justify paying extra on my mortgage with a rate that low since returns from shares will likely be at least double that, and since I’m very new on my FIRE journey think this is a great opportunity to kickstart my snowball. Thanks for all the great content!
No worries and thanks for sharing your experiences.
Inspiring progress AF! Is your debt somehow deducted from your net-worth? From this post I can see your net-worth as a sum of Shares, Cash, Property Equity and Super. Thanks for the awesome content! Chris
Cheers mate. Yes, the debt has already been taken into account. The only debt that’s missing from these updates is Mrs FB’s HECS debt which is around $17K (but it’s factored into these monthly numbers just not shown above)
Hi Aussie Firebug,
Been following your podcast and blog, you said in your podcast that if you have a chance to start over, your method of investing just VGS + VTS + VEU or VDHG, but your 2019 blog mentioned VAS + VTS + VEU is the option.
I saw the W-8BEN form, it does not seem complicated to me, it seems worth the MER that you spent over the years.
Just starting out, been reading a lot of boglehead’s recommended books and FIRE podcasts.
What percentage do you allocate for between VTS and VEU?
I’d probably go A200+VGS or just VDHG. Tbh it doesn’t make that much of a difference.
The W-8BEN form is not hard at all but when there are alternatives that don’t require it, the reduced complexity is probably worth the saved MER IMO. Each to their own though.
We are aiming for 15% for both VTS and VEU.
Cheers
Hi Aussie Firebug,
Love the content you put out, what an awesome month November was!
I’ve got a question,
I’m getting to investing into ETFs.
I would love for your advice on where you would start here?
Would you split, or dump all into one ETF starting out?
Would you diversify between VAS VTS and VEU?
Or dump all into Betashares 200 ETF?
Thanks,
Jo
I’m glad you’re digging the content Jo.
Really hard to say what I’d do without much context I’m sorry. What are your goals? It’s usually a good idea to work backwards from there. If I were starting out again, I would probably just go A200/VGS at 70/30 respectively. I wouldn’t worry about rebalancing at the start and would buy a lump sum of at least >$3K each month.
Hope that helps
Hi AFB,
Just reviewing your awesome returns. I may have missed it do you state somewhere in your blogs how much you are investing vs capital gains? If willing to share, was just interested on how much you have been able invest on a regular basis. Merry Christmas/NY!
Many thanks, Zoe
This is a great question. I actually should make a blog post on how much money we have put into the portfolio vs how much it has increased in value. Would be really interesting. I don’t actually know the answer off the top of my head tbh. Let me get back to you